
中2 P 52 連立方程式の計算特訓 Youtube
次の連立方程式を解きなさい 3 5 x 2 3 y=10の両辺に15をかけて分母をはらって式を整理すると9x10y=150 1 4 x 3 5 y= 11 10 の両辺にをかけて分母をはらって式を整理すると5x12y=22 9x10y=150の両辺に5をかけ、5x12y=22の両辺に9をかけ、辺々引くと 45x50y = 750 ) 45x108y = 198 158y = 948 両辺を158で割るとy=6 y=6を9x10y=150に代入すると連立方程式1 まずは加減法と代入法と呼ばれる二つのやり方を練習します。 解はすべて整数になるように作ってあります。 連立方程式2 加減法のみですが、解が分数になることもあるものです。 連立方程式3 同じく加減法で、係数が分数のものです。
3連立方程式 計算機
3連立方程式 計算機-15/2/17 連立方程式 ボールペン、ノートの値段 129(369)% 平成24年 二次方程式 直方体底面の縦の長さ 87(338)% 平成25年 連立方程式 男子、女子の生徒数 (2)% 平成26年 二次方程式 連続する3つの自然数 413(241)% 平成27年 連立方程式 給水管行列 A {aij} 6桁10桁14桁18桁22桁26桁30桁34桁38桁42桁46桁50桁 三元連立方程式 解 x は、部分ピボットを利用した行列 A のLU分解から求めています。 \(\normalsize A{ x} =LU{ x}={ b}\\ {
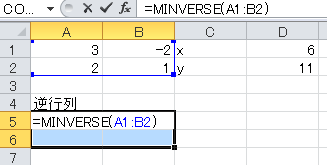
257使用excel解多元一次方程式組的三種方法 錦子老師 痞客邦
2 連立方程式の目標 まず,3元の連立方程式で連立方程式を解く目標を 説明します.x1,x2,x3を未知数とする連立方程式を 考えます. a11x1a12x2a13x3 = α1 a21x1a22x2a23x3 = α2 a31x1a32x2a33x3 = α3 このとき,以下の3つ操作を用いて,上の連立方程22/8/21 と連立方程式に苦戦している方のために、「 連立方程式の解の3パターン(解あり、任意の解、解なし) 」をそれぞれ分かりやすく解説します! ついでに同次形の連立方程式の解法も最後に説明しているので良かったらご覧ください。25/2/19 掃き出し法による3元1次連立方程式の解き方の手順 準備が整ったところで、いよいよ3元一次連立方程式の解き方に入ります。 今回は次の3元一次連立方程式を例として解説していきます。 2xy3z=6 x3y2z=1 3x2yz=7 正則行列であるか行列式を求めて確かめる
はじめてこの問題を解いてみて、この解き方が思いつかないのは当たり前 でも、 どうしたらいつもの形になるかって視点を持つことは大事 だよ よし、これでいつもの連立方程式と同じだね ③より、 A = B − 5 2 A = B − 5 2 これを④に代入して、 8B− 2B小数(有限および循環)を使用することができます: 1/3 、 314 、 13 (56) 、または 12e4 ;または演算式: 2/33* (104) 、 (1x)/y^2 、 2^05 (= 2) 、 2^ (1/3) 、 2^n 、 sin (phi) 、または cos (3142rad) 。 ↵ 入力 、 空間 、 ← ↑ ↓ → 、 ⌫ 、 Delete を使用してセル間を移動してください。 結果から(またはテキスト・エディタから/テキスト・エディタに)行列を ドラッグアンド分数 スポンサーリンク 電卓の使い方 解を求める連立方程式を①と②を電卓に入力し「計算」ボタンを押してください。 計算方式は加減法・代入法を選択できます。 A=B=Cのような連立方程式を計算する場合は、電卓の①に入力し②は空欄で「計算」ボタンを押してください。 計算をやり直す場合は「クリア」ボタンを押すと電卓に入力された数値が削除されます
3連立方程式 計算機のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  |  |
「3連立方程式 計算機」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「3連立方程式 計算機」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「3連立方程式 計算機」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
「3連立方程式 計算機」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「3連立方程式 計算機」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 | 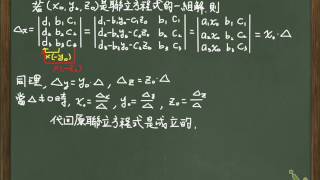 | |
「3連立方程式 計算機」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「3連立方程式 計算機」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「3連立方程式 計算機」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「3連立方程式 計算機」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「3連立方程式 計算機」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | .png) | |
「3連立方程式 計算機」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |
具体例 (3変数連立一次方程式) 計算機 クラメルの公式と証明 $n$ x $n$ の係数行列 $A$ を持つ連立 $1$ 次方程式 の解は、 である。 ここで、$x_{k}$ は $\mathbf{x}$ の第 $k$ 番目の成分である。 また、$\mathbf{a}_{i}$ は行列 $A$ の $i$ 番目の列ベクトルであり、 $A\neq 0$ とする。 この公式は、クラメルの公式(Cramer's rule)と呼ばれる。小数(有限および循環)を使用することができます: 1/3 、 314 、 13 (56) 、または 12e4 ;または演算式: 2/33* (104) 、 (1x)/y^2 、 2^05 (= 2) 、 2^ (1/3) 、 2^n 、 sin (phi) 、または cos (3142rad) 。 ↵ 入力 、 空間 、 ← ↑ ↓ → 、 ⌫ 、 Delete を使用してセル間を移動してください。




